Rib and Sea

Κείμενο και φωτογραφίες : Ιωσήφ Παπαδόπουλος.

Έχουμε μιλήσει μέχρι σήμερα για τη ναυτική διάλεκτο, το ανεμολόγιο, το ναυτικό camping, τους παράγοντες που πρέπει να λαμβάνει υπ’ όψιν του ο κάτοχος ενός φουσκωτού (και όχι μόνο) σκάφους όταν ταξιδεύει στη θάλασσα, αλλά δεν είπαμε τίποτε για τον τρόπο με τον οποίον μπορεί να υπολογίζει την πορεία του πάνω στον ναυτικό χάρτη. Και όπως έχω πολλές φορές τονίσει στο παρελθόν, κάθε κυβερνήτης σκάφους που σέβεται τον εαυτό του και τη θάλασσα, οφείλει να γνωρίζει, στοιχειωδώς, πώς να «διαβάζει» ένα ναυτικό χάρτη, πώς να υπολογίζει την πορεία και τη θέση του πάνω σ’ αυτόν.

Και πρέπει να διαθέτει αυτές τις στοιχειώδεις γνώσεις, ανεξαρτήτως εάν στο σκάφος του υπάρχει g.p.s., ραντάρ ή  οποιοδήποτε άλλο ηλεκτρονικό όργανο ναυσιπλοίας, για τον απλούστατο λόγο ότι οι ηλεκτρονικές συσκευές, με τον νόμο των πιθανοτήτων τουλάχιστον, παύουν ενίοτε να λειτουργούν. Είτε γιατί προκύπτει κάποιο ηλεκτρολογικής φύσεως πρόβλημα, είτε γιατί η ίδια η συσκευή υφίσταται κάποια ζημιά και τίθεται εκτός λειτουργίας.

Θα προσπαθήσω στη συνέχεια να δώσω, με όσο πιο απλό τρόπο μπορώ, τις απαραίτητες πληροφορίες, βάσει των οποίων ο αναγνώστης αυτού του άρθρου θα μπορέσει να κατανοήσει τα «μυστικά» του ναυτικού χάρτη, του διπαράλληλου, του κουμπάσου και της πυξίδας και, κάνοντας σωστή χρήση αυτών, να υπολογίζει κάθε φορά σωστά την πορεία και την θέση (στίγμα) του σκάφους του. Θα πρέπει βεβαίως, για να γίνει η όλη διαδικασία πιο απλή και ευχάριστη, να αντιμετωπίσετε τον υπολογισμό της πορείας και του στίγματος σαν παιγνίδι, παρά σαν αγγαρεία.

Οι ναυτικοί χάρτες έχουν τα δικά τους ιδιαίτερα χαρακτηριστικά που τους διαφοροποιούν από τους οδικούς. Στους ναυτικούς χάρτες αποτυπώνεται το υγρό περιβάλλον του πλανήτη και, κυρίως, οι παράλληλοι, οι μεσημβρινοί, τα νησιά, οι παράκτιες περιοχές, οι φάροι, τα θαλάσσια βάθη και το ανεμολόγιο. Τα στοιχεία τα οποία υπάρχουν πάνω σ’ ένα ναυτικό χάρτη, και τα οποία κυρίως μας ενδιαφέρουν προκειμένου να υπολογίσουμε την πορεία μας στη θάλασσα, είναι οι μεσημβρινοί και το ανεμολόγιο. Θα σας συνιστούσα να βάζετε τους ναυτικούς σας χάρτες σε ένα πλαστικό σωλήνα, σαν αυτούς που χρησιμοποιούν οι υδραυλικοί για τις αποχετεύσεις, κλείνοντας τα δύο άκρα του με βιδωτά καπάκια, ώστε να τους προφυλάσσετε από την υγρασία.

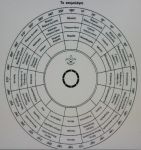Το ανεμολόγιο δεν είναι τίποτε άλλο παρά η απεικόνιση του ορίζοντα, η περιφέρεια του οποίου διαιρείται σε 360 πρώτα λεπτά (μοίρες) και φέρει δύο κάθετες διαμέτρους, εκ των οποίων η μία δείχνει την μεσημβρινή γραμμή, με άκρα της τα σημεία του ορίζοντα Βορράς – Νότος, η δε άλλη την γραμμή του πρώτου παραλλήλου, με άκρα της τα σημεία του ορίζοντα Ανατολή – Δύση. Ο δίσκος του ανεμολογίου διαιρείται ως εκ τούτου σε τέσσερα τεταρτημόρια, καθένα εκ των οποίων έχει 90 μοίρες (πρώτα λεπτά) και αντιστοιχεί σε ένα από τα τέσσερα βασικά σημεία του ορίζοντα. Θα πρέπει εδώ να αναφερθεί ότι οι ενδείξεις 0 (μηδέν) και 360 συμπίπτουν στον Βορρά, ενώ οι ενδείξεις 90 και 270 αντιστοιχούν στην Ανατολή και τη Δύση αντιστοίχως. Ανεμολόγια βλέπουμε αποτυπωμένα τόσο πάνω στους ναυτικούς χάρτες, όσο και στις μαγνητικές πυξίδες. Στο ανεμολόγιο του ναυτικού χάρτη σημειώνεται επίσης η παρατηρούμενη απόκλιση της περιοχής του συγκεκριμένου χάρτη, καθώς και η ετήσια μεταβολή αυτής της απόκλισης.

Τα όργανα που θα χρησιμοποιήσουμε για να υπολογίσουμε την πορεία και την απόσταση που πρόκειται να καλύψουμε, είναι ο διπαράλληλος και το κουμπάσο (ναυτικός "διαβήτης"). Λέγοντας διπαράλληλο εννοούμε ένα διπλό χάρακα, τα δύο σκέλη του οποίου μπορούν να απομακρύνονται και να κινούνται παράλληλα (το ένα απ’ το άλλο) με τη βοήθεια δύο (επίσης παράλληλα κινουμένων) συνδέσμων. Επειδή η χρήση του διπαράλληλου είναι πολλές φορές σχεδόν αδύνατη εν πλω, ιδίως όταν οι καιρικές συνθήκες δεν είναι ιδανικές (καθώς είναι δύσκολο να κρατήσουμε σταθερά και να κινήσουμε πάνω στον χάρτη τα δύο σκέλη του διπαράλληλου), είναι προτιμότερο ή να έχουμε φροντίσει να πλαστικοποιήσουμε τον χάρτη του ταξιδιού μας σε μέγεθος Α4, με προσημειωμένες πάνω του τις πορείες, ή να χρησιμοποιήσουμε ένα άλλο όργανο, πιο εύχρηστο, το οποίο κάνει την ίδια ακριβώς δουλειά που κάνει και ο διπαράλληλος.

Πρόκειται στην ουσία για ένα πλαστικό ανεμολόγιο, από το κέντρο του οποίου ξεκινά ένας χάρακας, τον οποίον στρέφουμε κάθε φορά προς την πορεία που θέλουμε να ακολουθήσουμε, και ο οποίος μπορεί να περιστρέφεται ελεύθερα πάνω στο πλαστικό αυτό ανεμολόγιο προς όλες τις κατευθύνσεις.

Ας δούμε όμως πρώτα με ποιο τρόπο υπολογίζουμε την πορεία μας όταν έχουμε στη διάθεσή μας ένα διπαράλληλο. Χαράζουμε, κατ’ αρχάς, με ένα μολύβι πάνω στον χάρτη την πορεία που θέλουμε να ακολουθήσουμε. Δεν γράφουμε ποτέ με ανεξίτηλο μελάνι (στυλό), ώστε να μπορέσουμε, αν χρειαστεί, να κάνουμε διορθώσεις ή αλλαγές. Ας υποθέσουμε λοιπόν ότι ξεκινάμε από την Ανάβυσσο και θέλουμε να πάμε στο Λιβάδι της Σερίφου. Χαράζουμε, με την βοήθεια ενός χάρακα και ενός μολυβιού, όσες γραμμές χρειαστούν, ενώνοντας τα σημεία απόπλου και κατάπλου μας (από την Ανάβυσσο μέχρι το Λιβάδι Σερίφου). Προσέχουμε, βεβαίως, να μην περάσει η γραμμή που θα χαράξουμε πάνω απ’ τα... βουνά και να βεβαιωθούμε ότι πάνω στην πορεία που χαράξαμε δεν υπάρχουν ύφαλοι και ξέρες!

Στο πρώτο τμήμα της συγκεκριμένης διαδρομής (μέχρις ότου βγούμε στο ανοικτό πέλαγος) δεν θα χρειαστεί να υπολογίσουμε την πορεία μας γιατί υπάρχει οπτική επαφή και παράλληλη πλεύση με τη στεριά. Στο σημείο αυτό θα ήθελα να σας ζητήσω, και να σας συστήσω, να μην περνάτε πολύ κοντά στις ακτές. Πρώτον, γιατί δεν το επιτρέπει ο Γενικός Κανονισμός Λιμένα και δεν είναι πολύ έξυπνο να πλέετε με ένα ταχύπλοο σκάφος κοντά στις παραλίες. Δεύτερον, γιατί υπάρχει ο κίνδυνος να περάσετε πάνω από κάποιον αμελή ψαροντουφεκά, ο οποίος δεν θα έχει φροντίσει να δηλώσει την παρουσία του με ένα πλωτήρα. Τρίτον, γιατί μπορεί ο άνεμος και τα κύματα να κινούνται προς τα βράχια της παραλίας, να υπάρχει αντιμάμαλο, κι’ εκείνη ακριβώς τη στιγμή να αποφασίσει ο κινητήρας του σκάφους σας να πάθει... συγκοπή! Φαντασθείτε λοιπόν να μείνετε ακυβέρνητος, και πάνω στον πανικό σας και τον χρόνο που θα χρειαστείτε μέχρι να ενεργοποιήσετε τον εφεδρικό κινητήρα (αν υπάρχει εφεδρικός κινητήρας, και αν ενεργοποιηθεί), να σας ρίξουν τα κύματα πάνω στα βράχια! Κρατάτε λοιπόν πάντοτε τόση απόσταση από τις ακτές, όση χρειάζεται για να σας δοθεί ο χρόνος να αντιδράσετε εγκαίρως και να μη θέσετε το σκάφος και τους επιβαίνοντες σε κίνδυνο, αν κάτι πάει στραβά.

Αφού φτάσουμε στο σημείο της γραμμής που χαράξαμε και έχουμε μπροστά μας το ανοικτό πέλαγος, ευθυγραμμίζουμε το ένα από τα σκέλη του διπαράλληλου πάνω στη χαραγμένη πορεία (ας το ονομάσουμε σκέλος Α), φροντίζοντας με το ένα χέρι μας να το κρατάμε σταθερά στη θέση του, απομακρύνοντας συγχρόνως το άλλο (ας το ονομάσουμε σκέλος Β) προς το ανεμολόγιο του χάρτη που βρίσκεται πιο κοντά. Τις περισσότερες φορές δεν αρκεί ένα άνοιγμα του διπαράλληλου για να φθάσουμε στο ύψος του πλησιέστερου ανεμολογίου. Κρατώντας λοιπόν σταθερό το σκέλος του διπαράλληλου που μετακινήσαμε στην αρχή (σκέλος Β), φέρνουμε κοντά του το άλλο (σκέλος Α) και επαναλαμβάνουμε την ίδια κίνηση έως ότου το σκέλος Β πέσει πάνω στο κέντρο του ανεμολογίου. Η ένδειξη που υπάρχει στο ανεμολόγιο είναι η πορεία που θα πρέπει να ακολουθήσουμε (σε μοίρες) μέχρι το ακρωτήριο του Κύκλωπα της Σερίφου. Σημειώνουμε αυτόν τον αριθμό με μολύβι πάνω στη γραμμή που χαράξαμε. Η υπόλοιπη διαδρομή μέχρι τον προορισμό μας (Λιβάδι) είναι παράκτια, υπάρχει οπτική επαφή με την στεριά και, συνεπώς, δεν είναι απαραίτητο να υπολογίσουμε την πορεία μας σε μοίρες. Αυτό θα το κάναμε εάν η Σέριφος ήταν στη... Σκωτία, όπου η ομίχλη είναι καθημερινό σχεδόν φαινόμενο!

Δεν θα χρειαστεί να ακολουθήσετε την ίδια διαδικασία για να υπολογίσετε την πορεία της επιστροφής σας. Εφ’ όσον επιλέξετε την ίδια ρότα (έτσι λέμε στη θάλασσα την διαδρομή που ακολουθεί το σκάφος), δεν έχετε παρά να κάνετε τον εξής πολύ απλό υπολογισμό. Εάν μεν η πορεία του πηγαιμού σας ήταν από 1 μέχρι και 180 μοίρες, τότε θα προσθέσετε στον αριθμό αυτόν το 180 και θα έχετε την πορεία της επιστροφής. Εάν η πορεία του πηγαιμού σας ήταν από 181 μέχρι και 360 μοίρες, θα αφαιρέσετε τον αριθμό 180 και θα έχετε την πορεία της επιστροφής.

Παράδειγμα : Ας υποθέσουμε ότι η πορεία σας από τον Πάτροκλο μέχρι τον κάβο του Κύκλωπα στη Σέριφο είναι 146 μοίρες Ν.Α. (δηλαδή κάτω από 180 μοίρες). Για να υπολογίσετε την πορεία της επιστροφής σας από τον κάβο του Κύκλωπα μέχρι τον Πάτροκλο, δεν έχετε παρά να προσθέσετε 180 μοίρες. Δηλαδή 146 + 180 = 326 μοίρες Β.Δ. Αντιθέτως, εάν υποθέσουμε ότι αποπλεύσατε από την Ανάβυσσο με προορισμό την Ύδρα και η πορεία σας ήταν 225 μοίρες Ν.Δ. (δηλαδή πάνω από 180), για να υπολογίσετε την πορεία της επιστροφής σας δεν έχετε παρά να αφαιρέσετε τον αριθμό 180. Δηλαδή 225 – 180 = 45 μοίρες Β.Α.

Πώς όμως χρησιμοποιούμε το όργανο της ένθετης φωτογραφίας για να υπολογίσουμε την πορεία μας; Εδώ τα πράγματα είναι πολύ πιο απλά και δεν θα χρειαστούμε το ανεμολόγιο του χάρτη, για τον απλούστατο λόγο ότι το ίδιο το όργανο αυτό είναι ανεμολόγιο. Το τοποθετούμε λοιπόν με τέτοιο τρόπο, ώστε το κέντρο του ανεμολογίου να συμπέσει με το σημείο του απόπλου μας. Είναι πολύ βασικό να προσέξουμε ώστε ο Βορράς, που απεικονίζεται συνήθως στο πλαστικό ανεμολόγιο του οργάνου με το γράμμα «Ν» (από την αγγλική λέξη "North") να είναι πάντοτε απέναντι από τον Βορρά του ναυτικού χάρτη, και οι γραμμές του τετράγωνου πλαισίου του οργάνου να είναι παράλληλες με τους μεσημβρινούς και τους παραλλήλους της γης, που απεικονίζονται στον ναυτικό χάρτη με κάθετες και παράλληλες αντιστοίχως γραμμές. Κρατώντας τώρα σταθερά με το ένα χέρι μας το πλαστικό ανεμολόγιο στη θέση αυτή, στρέφουμε τον χάρακα μέχρις ότου ευθυγραμμιστεί και συμπέσει με το σημείο του προορισμού μας. Ο αριθμός του πλαστικού ανεμολογίου με τον οποίον ευθυγραμμίζεται ο χάρακας είναι η πορεία μας.

Πάνω στα ανεμολόγια του ναυτικού χάρτη σημειώνονται, όπως ήδη ανέφερα πιο πάνω, η απόκλιση της συγκεκριμένης περιοχής του χάρτη και η ετήσια μεταβολή της. Δεν θα ήθελα να σας μπερδέψω όμως με υπολογισμούς, γιατί θεωρώ ότι όσο τα ταξίδια σας περιορίζονται στο Αιγαίο, όπου οι αποστάσεις μεταξύ των νησιών του είναι σχετικώς μικρές, και οι χάρτες που χρησιμοποιείτε είναι σύγχρονοι και ενημερωμένοι, δεν χρειάζεται να μπείτε στον κόπο να υπολογίσετε την απόκλιση της περιοχής του χάρτη και την ετήσια μεταβολή αυτής της απόκλισης. Ο υπολογισμός της απόκλισης είναι απαραίτητος όταν χρειάζεται να κροσάρουμε μεγάλα θαλάσσια ανοίγματα. Ανάλογα με την παλαιότητα του χάρτη μεταβάλλεται και ο βαθμός απόκλισης.

Για την ιστορία, πάντως, και κυρίως γι' αυτούς που είναι σχολαστικοί και τελειομανείς, θα αναφέρω μερικά στοιχεία. Όταν η απόκλιση είναι προς ανατολάς, είναι προσθετική ενώ, όταν είναι προς δυσμάς, είναι αφαιρετική. Για να γίνει περισσότερο κατανοητό αυτό και για να δούμε με ποιο τρόπο υπολογίζουμε την απόκλιση, ας υποθέσουμε ότι η απόκλιση που σημειωνόταν στο ανεμολόγιο ενός ναυτικού χάρτη του 1999 ήταν 2 μοίρες ανατολικά και θα αυξανόταν κατά 7 πρώτα λεπτά ετησίως. Αυτό σημαίνει ότι το 1999 η απόκλιση μεταξύ του πραγματικού και του μαγνητικού βορρά, στο συγκεκριμένο σημείο του χάρτη, ήταν 2 μοίρες και από τότε θα ηύξανε κατά 7 πρώτα λεπτά τον χρόνο. Αν χρησιμοποιούσαμε σήμερα αυτόν τον ναυτικό χάρτη, θα έπρεπε στην απόκλιση των 2 μοιρών να προσθέσουμε την αύξηση των 7 πρώτων λεπτών για κάθε χρόνο μέχρι το 2010, δηλαδή επί 11 χρόνια. Τότε η απόκλιση θα ήταν : 2 μοίρες + 7΄ Χ 11 (77 πρώτα λεπτά, ήτοι 1 μοίρα και 17 πρώτα λεπτά της μοίρας) = 3 μοίρες και 17 πρώτα λεπτά της μοίρας. Στην πράξη δεν χρειάζεται να το κάνουμε αυτό, γιατί οι ναυτικοί χάρτες που χρησιμοποιούμε στις μέρες μας είναι νεώτερης έκδοσης (έτσι τουλάχιστον πρέπει) και συνεπώς ο υπολογισμός  της αύξησης ή της ελάττωσης της απόκλισης γίνεται συνήθως για περίοδο τριών έως τεσσάρων ετών και είναι πολύ μικρή. Γι' αυτό είπα στην αρχή αυτής της ενότητας πως δεν θεωρώ ότι είναι απαραίτητο να λαμβάνουμε υπ' όψη μας την απόκλιση όταν υπολογίζουμε την πορεία μας, στο Αιγαίο τουλάχιστον, όπου οι αποστάσεις μεταξύ των νησιών είναι πολύ μικρές.

Και αφού υπολογίσαμε την πορεία μας, ήρθε η ώρα να μετρήσουμε την απόσταση που πρόκειται να καλύψουμε. Οι αποστάσεις στη θάλασσα μετρώνται πάντοτε σε ναυτικά μίλια. Το ναυτικό μίλι ισούται με 1.852 μέτρα. Δεν θα μπω στη διαδικασία να σας πω με ποιο τρόπο υπολογίστηκε ότι το ναυτικό μίλι ισούται με 1.852 μέτρα, γιατί την απάντηση μπορείτε εύκολα να την πάρετε αν την αναζητήσετε σε κάποια από τις μηχανές αναζήτησης του διαδικτύου. Αν μάλιστα διστάσατε στην αρχή να ξεκινήσετε την ανάγνωση αυτού του άρθρου, δεν θα ήθελα, περιγράφοντας πολύπλοκους μαθηματικούς υπολογισμούς να γίνω η αιτία που θα σας κάνει να το παρατήσετε στη μέση!

Προσέξτε, πάντως, γιατί είναι άλλο πράγμα να λέμε ότι η απόστασή μας από τον Πάτροκλο μέχρι τον Κάβο του Κύκλωπα στη Σέριφο είναι 38 ν. μίλια, και άλλο πράγμα να λέμε ότι το σκάφος μας πλέει με 38 ν. μίλια την ώρα. Στην πρώτη περίπτωση αναφερόμαστε σε μονάδα μέτρησης της απόστασης, ενώ στη δεύτερη περίπτωση αναφερόμαστε σε μονάδα μέτρησης της ταχύτητας. Όταν μάλιστα μιλάμε για ταχύτητα, είναι πιο σωστό να λέμε ότι το σκάφος μας πλέει με 38 κόμβους, αντί να λέμε ότι πλέει με 38 ν. μίλια την ώρα. Όπου κόμβος, σαν μονάδα μέτρησης της ταχύτητας, είναι η απόσταση σε ν. μίλια που καλύπτει το σκάφος μας σε μία ώρα.

Για να υπολογίσουμε λοιπόν πάνω στον ναυτικό χάρτη την απόσταση που πρόκειται να διανύσουμε, δεν έχουμε παρά να τοποθετήσουμε το ένα άκρο του κουμπάσου (ναυτικός "διαβήτης") στο σημείο από όπου υπολογίσαμε την αρχή της πορείας μας (κοντά στον Πάτροκλο), και το άλλο άκρο του στον κάβο του Κύκλωπα. Στη συνέχεια μεταφέρουμε το άνοιγμα αυτό του κουμπάσου σε έναν από τους δύο μεσημβρινούς του χάρτη (οι κάθετες γραμμές που απεικονίζονται στα δύο άκρα του) και κατά προτίμηση στο ύψος του μεσημβρινού που βρίσκεται πλησιέστερα προς το ύψος της περιοχής που θέλουμε να μετρήσουμε. Αυτό το κάνουμε γιατί, λόγω της καμπυλότητας και του ελλειπτικού σχήματος της γης, το μήκος του ν. μιλίου δεν είναι το ίδιο σε όλα τα γεωγραφικά πλάτη. Προσοχή! Δεν μετράμε ποτέ την απόσταση κάνοντας χρήση των παραλλήλων του χάρτη που βρίσκονται στο επάνω και κάτω άκρο του. Οι υποδιαιρέσεις των παραλλήλων αυτών εκφράζουν το γεωγραφικό μήκος των διαφόρων τόπων από τον πρώτο Μεσημβρινό και πρέπει να γνωρίζουμε ότι δεν μπορούμε, ούτε και πρέπει, να μετράμε τις αποστάσεις πάνω σ’ αυτές.

Βλέπουμε λοιπόν ότι αν τοποθετήσουμε το ένα άκρο του κουμπάσου στον μεσημβρινό που αντιστοιχεί στις 38 μοίρες, το άλλο άκρο του θα δείξει 37 μοίρες και 22 πρώτα λεπτά. Υπάρχει δηλαδή μεταξύ των δύο αυτών ενδείξεων μια διαφορά 38 πρώτων λεπτών. Έχοντας στο μυαλό μας ότι κάθε μοίρα έχει 60 πρώτα λεπτά, κάθε πρώτο λεπτό ισοδυναμεί με μία μοίρα και κάθε μοίρα με ένα ν. μίλι, καταλήγουμε στο συμπέρασμα ότι η απόσταση που μας χωρίζει από τον Πάτροκλο μέχρι τον κάβο του Κύκλωπα είναι 38 ν. μίλια.

Την πορεία που υπολογίσαμε θα την ακολουθήσουμε παρατηρώντας την πυξίδα. Η βελόνα της πυξίδας, που έχουμε στα φουσκωτά σκάφη μας, δείχνει τον μαγνητικό βορρά και γι’ αυτό η πυξίδα ονομάζεται μαγνητική. Τον πραγματικό ή αληθή βορρά δείχνουν μόνο οι γυροσκοπικές πυξίδες των πλοίων. Πολλές φορές, και ιδίως τα τελευταία χρόνια που τα σκάφη μας εξοπλίστηκαν με διάφορα ηλεκτρονικά «καλούδια», όργανα, ραδιοκασετόφωνα κ.λπ., οι πυξίδες επηρεάστηκαν και άρχισαν να «τρελλαίνονται», δείχνοντας αντί για τον μαγνητικό βορρά, τον δικό τους βορρά, τον λεγόμενο βορρά της πυξίδας. Αυτή η «τρέλλα» της πυξίδας, οι λανθασμένες ενδείξεις της (εξ αιτίας της γειτνίασής της με όλα τα «καλούδια» που λίγο πιο πριν ανέφερα) και η γωνία που σχηματίζεται μεταξύ μαγνητικού βορρά και βορρά πυξίδας, ονομάζεται παρεκτροπή.

Την παρεκτροπή μπορούμε να την υπολογίσουμε ή ακόμη και να την διορθώσουμε, αφού οι περισσότερες σύγχρονες πυξίδες διαθέτουν ρυθμιζόμενους μαγνήτες και παρέχουν αυτή την δυνατότητα. Δεν είναι όμως του παρόντος να εξηγήσω πώς γίνεται αυτό και αν δεν γνωρίζετε πώς να το κάνετε, μην το επιχειρήσετε. Υπάρχουν ειδικοί, οι οποίοι γνωρίζουν ακριβώς πώς πρέπει να γίνει η διόρθωση της παρεκτροπής μιας μαγνητικής πυξίδας και σ' αυτούς πρέπει να αποτανθείτε. Θα προσπαθήσω να μιλήσω στο μέλλον με έναν από αυτούς και θα σας μεταφέρω τις απόψεις του.

Πρέπει βεβαίως να πω ότι ο βαθμός παρεκτροπής μιας μαγνητικής πυξίδας μπορεί να είναι διαφορετικός από βορρά προς νότον και διαφορετικός από ανατολάς προς δυσμάς. Σήμερα, πάντως, την διαπίστωση και τον υπολογισμό της παρεκτροπής της μαγνητικής πυξίδας μπορούμε να την κάνουμε πολύ πιο εύκολα με την χρήση του g.p.s. Να πώς.

Αφού υπολογίσουμε την πορεία μας πάνω στον ναυτικό χάρτη με την βοήθεια του διπαράλληλου, παίρνουμε ένδειξη της ίδιας πορείας από το g.p.s. Παρατηρούμε τότε ότι, ενώ το g.p.s. συμφωνεί με την πορεία των 146 μοιρών που έχουμε προϋπολογίσει από τον Πάτροκλο προς τον Κάβο του Κύκλωπα, όταν ακολουθήσουμε αυτή την πορεία στη θάλασσα η βελόνα της πυξίδας μας δείχνει π.χ. 135 μοίρες. Με δεδομένο ότι η ένδειξη του g.p.s. είναι η σωστή, διαπιστώνουμε ότι η παρεκτροπή της πυξίδας μας, για την συγκεκριμένη κατεύθυνση, είναι 11 μοίρες. Δεν έχουμε λοιπόν παρά να ακολουθήσουμε την ένδειξη της πυξίδας (135 μοίρες) αφού έχουμε ήδη βεβαιωθεί ότι, αν δεν υπήρχε λόγος να παρεκτραπεί, θα συμφωνούσε προφανώς με την ένδειξη 146 του g.p.s. και την πορεία που εμείς υπολογίσαμε με την χρήση του διπαράλληλου.

Αυτό έκανα κι’ εγώ τα τελευταία χρόνια όταν, ταξίδευα μεν βάσει του ναυτικού χάρτη και της πυξίδας, είχα όμως στο σκάφος μου και ένα g.p.s. για τέτοια ενδεχόμενα. Η διαπίστωση και ο υπολογισμός της παρεκτροπής της πυξίδας είναι άλλωστε ένας αρκετά σοβαρός λόγος για τον οποίον, κατά την γνώμη μου, το g.p.s. μπορεί να φανεί ιδιαιτέρως χρήσιμο. Το θέμα δεν είναι, με άλλα λόγια, πώς θα κάνουμε τυφλοσούρτη το g.p.s. προκειμένου να ταξιδεύσουμε στη θάλασσα, αλλά πώς θα το εκμεταλλευτούμε για να κάνουμε αφ’ ενός μεν τη ζωή μας ευκολότερη σαν άνθρωποι της θάλασσας, αφ’ ετέρου να μην ξεχάσουμε αυτά που μάθαμε, ώστε να συνεχίσουμε να ταξιδεύουμε, αν συμβεί κάποτε και το g.p.s. παύσει για κάποιο λόγο να λειτουργεί.

Ας δούμε τώρα με ποιους τρόπους μπορούμε να υπολογίσουμε τη θέση μας πάνω στον ναυτικό χάρτη. Η θέση του σκάφους μας πάνω στον χάρτη σε κάποια συγκεκριμένη στιγμή ονομάζεται στίγμα. Αυτό, εκ πρώτης όψεως, φαίνεται εύκολο να το υπολογίσουμε, γιατί αφού μάθαμε πώς χαράσσουμε την πορεία μας πάνω στον χάρτη και πώς μπορούμε να μετρήσουμε την απόσταση που χωρίζει το σημείο απ’ το οποίο αποπλεύσαμε μέχρι το σημείο που θέλουμε να καταπλεύσουμε, μπορούμε να προσδιορίσουμε σε ποιο σημείο της ρότας του σκάφους μας βρισκόμαστε μια ωρισμένη χρονική στιγμή. Αρκεί να πολλαπλασιάσουμε τον χρόνο που πέρασε, από την ώρα του απόπλου, με την ωριαία ταχύτητα του σκάφους και να βρούμε πόσα μίλια διανύσαμε.

Το σκάφος όμως, για διαφόρους λόγους, δεν είναι δυνατόν να κρατηθεί σταθερά πάνω στην προσχεδιασμένη πορεία του. Είτε γιατί πλαγιολισθαίνει (ξεπέφτει από την πορεία του) λόγω ισχυρών πλευρικών ανέμων και ρευμάτων, είτε γιατί η πυξίδα του παρουσιάζει σφάλματα, είτε γιατί λόγω κακών καιρικών συνθηκών η ταχύτητά του μεταβάλλεται, είτε γιατί ο κυβερνήτης κοιτάζει περισσότερο την... όμορφη συνοδό του και λιγότερο την πυξίδα!

Σε μια τέτοια περίπτωση, αν μεν έχουμε οπτική επαφή με την ξηρά, μπορούμε να υπολογίσουμε τη θέση μας από τα σημάδια που έχει και ο χάρτης μας. Αυτό το επιτυγχάνουμε με τις λεγόμενες ευθυγραμμίσεις και διοπτεύσεις. Πότε όμως λέμε ότι είμαστε ευθυγραμισμένοι με ένα σημείο; Ας υποθέσουμε ότι διακρίνουμε στον ορίζοντα τον κάβο ενός μεγάλου σχετικώς νησιού και μπροστά από αυτόν ένα νησάκι με φάρο. Όταν το σκάφος μας περάσει μπροστά απ’ τον φάρο του μικρού νησιού, ώστε ο κάβος του μεγάλου νησιού, ο φάρος του μικρού νησιού και το σκάφος μας να βρεθούν στην ίδια ευθεία, τότε λέμε ότι είμαστε σε ευθυγράμμιση με τον κάβο και τον φάρο. Στην προέκταση της νοητής γραμμής, που ενώνει τον κάβο με τον φάρο, και σε κάποιο σημείο της βρίσκεται το σκάφος μας. Για να μπορέσουμε να χρησιμοποιήσουμε κάβους, νησάκια, κτίρια και άλλα αντικείμενα της ξηράς, προκειμένου να ευθυγραμμιστούμε μ’ αυτά και να υπολογίσουμε την θέση μας, πρέπει αυτά, όπως ήδη είπα, να είναι σημειωμένα και στον χάρτη μας.

Μπορούμε ακόμη να πάρουμε περισσότερες από μία ευθυγραμμίσεις, οπότε στα σημεία που οι νοητές ευθείες μεταξύ των ευθυγραμμίσεων τέμνονται, βρίσκεται και το στίγμα μας. Ας υποθέσουμε ότι ταξιδεύουμε ανοικτά της Αίγινας και βλέπουμε τον κάβο του Τούρλου σε ευθυγράμμιση με τον κάβο Κόγχη της Σαλαμίνας. Την ίδια στιγμή βλέπουμε τον κάβο Πύργο της Αίγινας σε ευθυγράμμιση με το νότιο άκρο της νησίδας Αγκίστρι. Αν τραβήξουμε στον χάρτη με μολύβι μια γραμμή που να ενώνει τον Τούρλο με την Κόγχη και άλλη μια που να ενώνει τον Πύργο με το νότιο άκρο του Αγκιστρίου, αυτές οι δύο γραμμές θα συναντηθούν σε κάποιο σημείο. Αν απ' το σημείο αυτό χαράξουμε (πάντοτε με μολύβι) δύο κάθετες γραμμές, μία προς τον μεσημβρινό (κάθετος γραμμή στο αριστερό ή δεξιό άκρο του χάρτη) και μία προς τον παράλληλο (παράλληλη γραμμή στο επάνω ή κάτω άκρο του χάρτη) θα βρούμε και το στίγμα μας, το οποίο θα είναι : 37 μοίρες 40΄ Βόρειο, 23 μοίρες 40΄ Ανατολικό.

Πώς όμως "διαβάζουμε" αυτό το στίγμα; Το στίγμα μας καθορίζεται από την θέση που έχει το σκάφος μας κάθε στιγμή πάνω στην υδρόγειο και είναι το σημείο όπου συναντώνται ένας συγκεκριμένος μεσημβρινός και ένας συγκεκριμένος παράλληλος. Έχοντας δηλαδή επισημάνει με τις ευθυγραμμίσεις και τις διοπτεύσεις σε ποιο σημείο της πορείας μας βρισκόμαστε, σημειώνουμε αυτό το σημείο με ένα μολύβι πάνω στον χάρτη. Στη συνέχεια, με αφετηρία το σημείο που βρισκόμαστε, χαράζουμε μία κάθετη γραμμή προς τον μεσημβρινό που απεικονίζεται στο αριστερό ή δεξιό άκρο του χάρτη, και άλλη μία γραμμή προς τον παράλληλο που απεικονίζεται στο επάνω ή κάτω άκρο του χάρτη, και διαβάζουμε τις δύο ενδείξεις. Έτσι προέκυψαν οι αριθμοί που βρήκαμε λίγο νωρίτερα στην αναζήτηση της θέσης μας ανοικτά της Αίγινας. 

Αν θέλουμε τώρα να υπολογίσουμε με μεγαλύτερη ακρίβεια τη θέση μας, θα πρέπει να καταφύγουμε στη λήψη διοπτεύσεων (αζιμούθιο). Διόπτευση είναι η σκόπευση ενός ωρισμένου σημείου της ξηράς (που πρέπει να το περιλαμβάνει και ο χάρτης μας) ώστε να βρούμε στις πόσες μοίρες της πυξίδας βλέπουμε το σημείο αυτό. Ας υποθέσουμε ότι ταξιδεύουμε νοτιοανατολικά της Σίφνου, με κατεύθυνση προς την Ίο, και κάποια στιγμή διακρίνουμε το νότιο άκρο της Αντιπάρου σε ευθυγράμμιση με τον νότιο κάβο της Πάρου. Δεν βλέπουμε όμως άλλη ευθυγράμμιση ώστε σε συνδυασμό με την πρώτη να υπολογίσουμε το στίγμα μας, όπως στο προηγούμενο παράδειγμα. Έχουμε δηλαδή μία μόνο ευθυγράμμιση και γνωρίζουμε ότι κάπου επάνω στη νοητή αυτή γραμμή της πορείας μας είναι η θέση του σκάφους μας. Χρειάζεται λοιπόν, με κάποιο τρόπο, να βρούμε σε ποιο σημείο της νοητής αυτής γραμμής βρισκόμαστε, γιατί στην περίπτωση αυτή η απόστασή μας από την Αντίπαρο και την Πάρο είναι μεγάλη και δεν μπορούμε να την υπολογίσουμε με το μάτι, όπως κάναμε στην απλή ευθυγράμμιση.

Παρατηρώντας την πυξίδα μας (οι φορητές πυξίδες διόπτευσης είναι πιο βολικές, αντί να στρέφουμε την πλώρη του σκάφους μας προς τον ζητούμενο στόχο) βλέπουμε το κέντρο περίπου της Πολυαίγου στις 235 μοίρες. Αν τραβήξουμε μία γραμμή στον χάρτη, που να περνάει από την Πολύαιγο και να έχει διεύθυνση τις 235 μοίρες του ανεμολογίου, τότε η γραμμή αυτή θα συναντήσει σε ένα σημείο την ευθυγράμμισή μας με την Αντίπαρο και την Πάρο. Αυτό το σημείο θα είναι το στίγμα μας, γιατί είναι το μόνο σημείο επάνω στην ευθυγράμμιση από όπου η Πολύαιγος φαίνεται στις 235 μοίρες. Απαραίτητη προϋπόθεση, για μια τέτοια διόπτευση, είναι να έχουμε υπολογίσει ή διορθώσει τις παρεκτροπές της πυξίδας μας. Εννοείται επίσης ότι για να χαράξουμε μια τέτοια γραμμή, δηλαδή παράλληλη με μια άλλη που να περνάει απ’ το κέντρο του ανεμολογίου και τις 235 μοίρες, πρέπει να χρησιμοποιήσουμε τον διπαράλληλο, όπως κάναμε και κατά την χάραξη της πορείας.

Για να πούμε πάντως και του στραβού το δίκιο, όλα αυτά είναι "περιττά" εάν στο σκάφος υπάρχει (και λειτουργεί) g.p.s. Κανείς (ούτε κι’ εγώ) δεν μπορεί να αμφισβητήσει τους θαλάσσιους δρόμους που άνοιξε σε όλους (ναυτικούς και, κυρίως, άναυτους) αυτό το ηλεκτρονικό σύστημα παγκοσμίου εντοπισμού θέσης (g.p.s.). Επειδή ωστόσο επιμένω και θέλω να είμαι «on the safe side», όπως λένε οι Άγγλοι, θα συνεχίσω να βασίζομαι στον κλασσικό τρόπο ναυσιπλοίας, έχοντας σαν «back up» την σύγχρονη τεχνολογία. Η μέχρι σήμερα πορεία μου και η ερωτική σχέση μου μαζί Της, με έχουν πείσει ότι η επιλογή μου αυτή είναι η πιο σωστή και η πιο συναρπαστική...